Trees

Tutorials
/
Interviewing
/
Trees
Previous:
Linked Lists
Next:
Graphs

Trees

So far, you’ve learned about a lot of data structures that are built into Java: arrays, maps, sets, queues, and stacks. You’ve also learned about the first node-based data structure: linked lists.

Link lists are composed of nodes. Each node contains a value and points to a single child node:

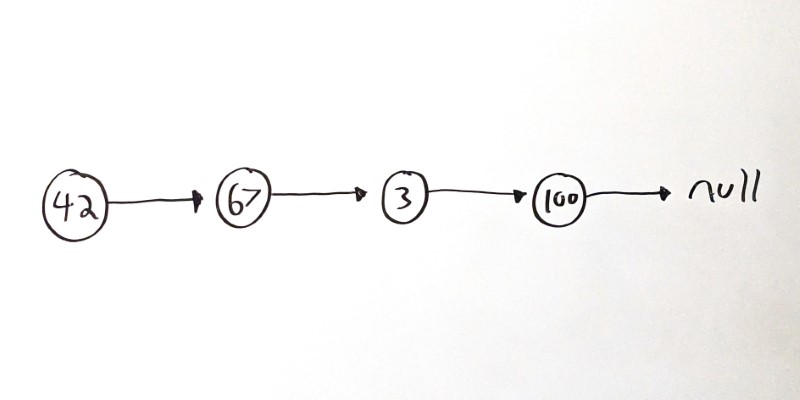
Visualization of 4 nodes in a linked list. Each node points to the next node, except for the last node which points to null.

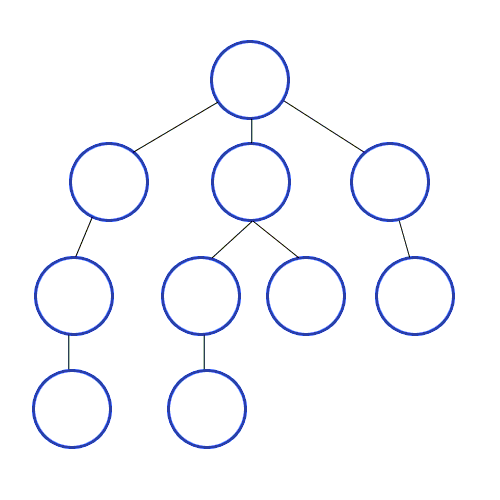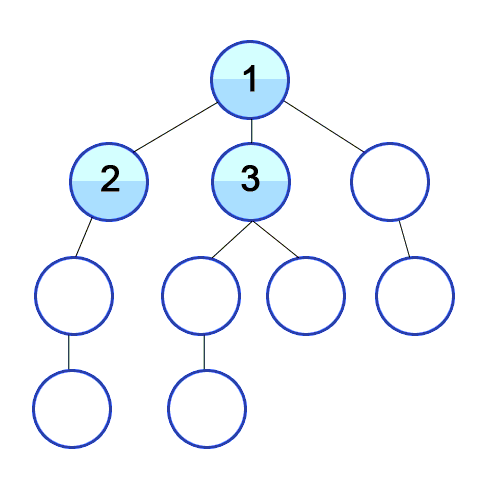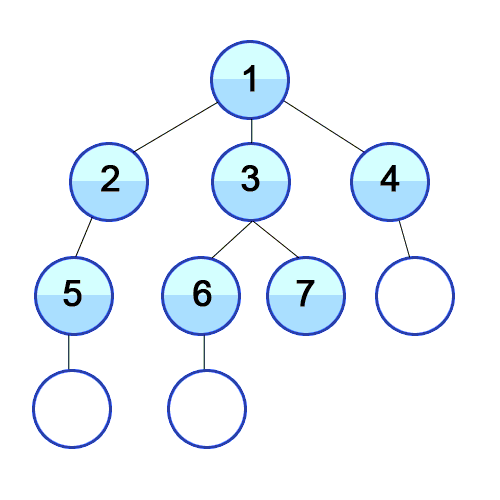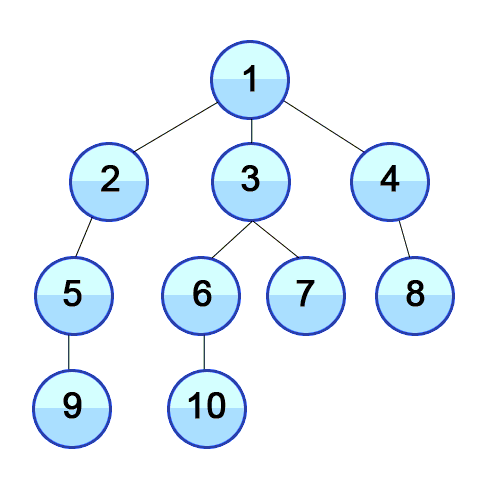
Trees are very similar, except each node can point to multiple child nodes!

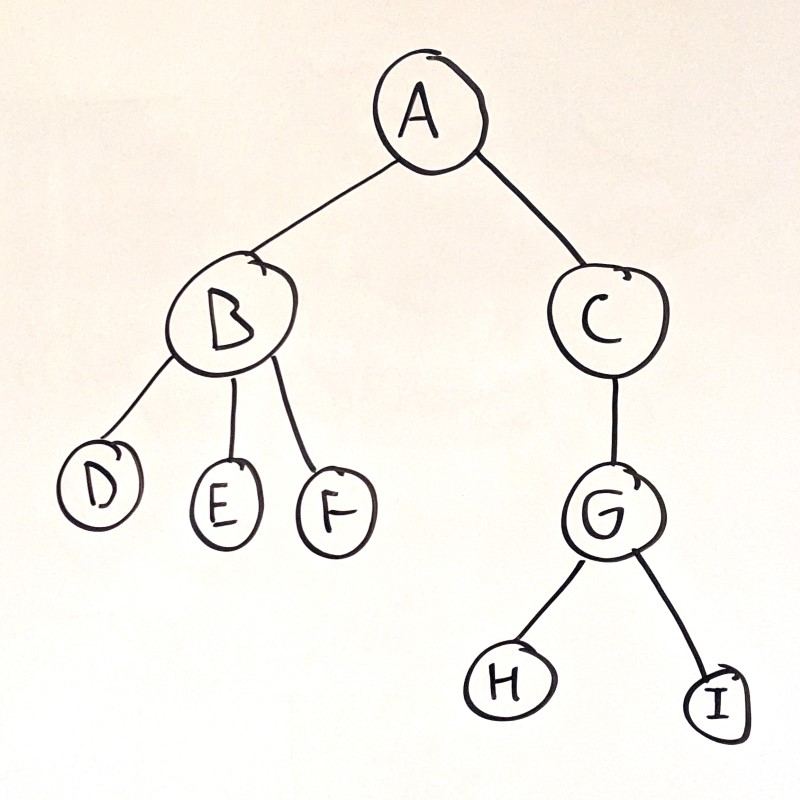
In this example, node A points to two child nodes: node B and node C. Node B has three child nodes D, E, and F. Node C has a single child node G, which has two child nodes H and I.

Putting this into code, you might represent a tree using this Node class:

class Node {
  Object value; // Can be int, String, etc.
  List<Node> children;
}

Often, trees contain nodes that have at most two children, also called a binary tree. Binary trees can be represented by this Node class:

class Node {
  Object value; // Can be int, String, etc.
  Node leftChild;
  Node rightChild;
}

Why Trees

Trees are useful for storing hierarchical data like directory structures, XML or HTML content, family relationships, or phylogenetic categorization. They’re also useful for storing data in a way that’s easier to navigate, or for representing decision-making processes.

Most other data structures we’ve studied are handy because they improve the efficiency of specific types of problems. And although trees can improve the efficiency of certain types of problems, their main benefit is unlocking a new way of thinking about problems in the first place.

For example, let’s say I have this directory structure on my computer:

  • C:/
    • Desktop/
      • Code/
        • HelloWorld.java
        • Test.java
      • cat.jpg
    • Documents/
      • post.txt
      • resume.pdf

You could probably represent this using an array if you really wanted to. But a tree data structure is much more natural to work with!

Binary Search Trees

Remember that if you have an array of sorted data, you can use binary search to find the index of an element in O(log n) time complexity.

Binary search trees are designed with the same idea in mind. A binary search tree is a tree where each node has a value and two children, but with a very important property: every value underneath the left child is less than the parent node’s value, and every value underneath the right child is greater than the parent node’s value.

class Node {
  int value;

  // Values under this node are less than value.
  Node leftChild;

  // Values under this node are greater than value.
  Node rightChild;
}

Here’s an example:

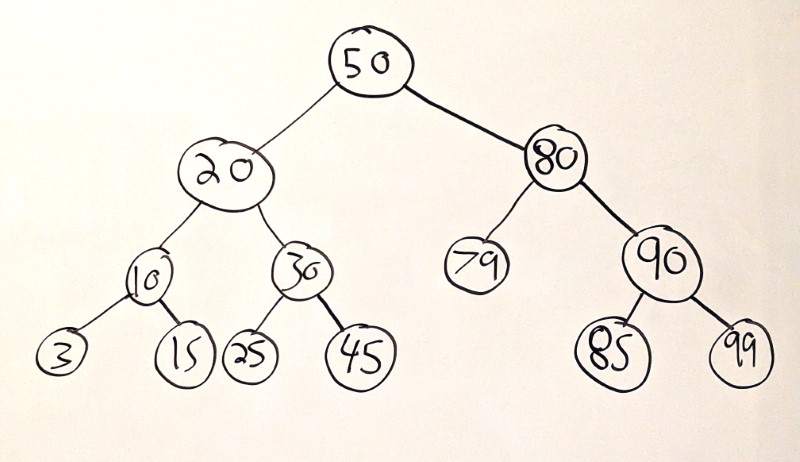
Like the name suggests, binary search trees are designed to make searching easier. To find 45 in the above tree, you’d follow this algorithm:

  • Start at the root. 45 is less than 50, so traverse to the left child.
  • 45 is greater than 20, so traverse to the right child.
  • 45 is greater than 30, so traverse to the right child.
  • We found 45. And it only took 4 steps!

Binary search trees are very common in interview questions, so make sure you’re familiar with them!

Remember: Binary search trees are common, but not every tree is a binary search tree, or even a binary tree! Trees come in all shapes and sizes. 🌲🌳🌴🎄🎋

Tree Traversal

No matter what kind of tree you have, you’ll have to traverse it by navigating from parent nodes to child nodes.. There are a few different ways to do this, and being able to talk about them is a great way to impress your interviewer.

Here are a couple approaches for traversing a tree:

With depth-first search, you search through an entire child subtree before you search another child subtree. In other words, you search down before you search across.

animation showing 10 nodes being explored via depth-first search

Depth-first search is often implemented using recursion:

class Node {
  Object value;
  List<Node> children;
}


void depthFirstSearch(Node node) {
  // Base case, just in case.
  if (node == null) {
    return;
  }

  // Do something with the current node.
  System.out.println(node.value);

  // Explore each subtree completely.
  for (Node child : node.children) {
    depthFirstSearch(child);
  }
}

You can also use a stack to implement depth-first search iteratively:

void depthFirstSearchIterative(Node head) {
  Deque<Node> nodeStack = new ArrayDeque<>();
  nodeStack.push(head);

  while (!nodeStack.isEmpty()) {
    Node node = nodeStack.pop();

    // Do something with the current node.
    System.out.println(node.value);

    // Add each child to the stack.
    for (Node child : node.children) {
      nodeStack.push(child);
    }
  }
}

Depth-first search is handy when you know you need to search the entire tree.

Traversal Order

Depth-first search traverses the tree by exploring one child’s subtree before exploring another child’s subtree.

But you can specify the order that you visit children. Here are a few common techniques:

  • Pre-order traversal takes some action for the current node, and then traverses to the node’s children.
  • Post-order traversal first traverses to a node’s children, and then takes some action for the current node.
  • In a binary tree, in-order traversal first visits a node’s left child, and then takes some action for the current node, and then visit the node’s right child.
  • You can also reverse the order of any of the above!

The order that you visit nodes depends on the problem. In an interview, talk through your options and the pros and cons of each approach.

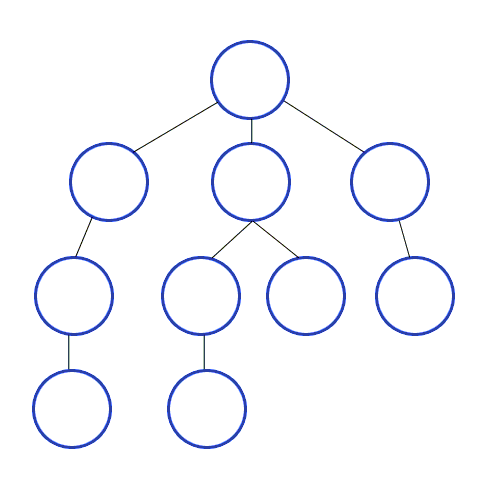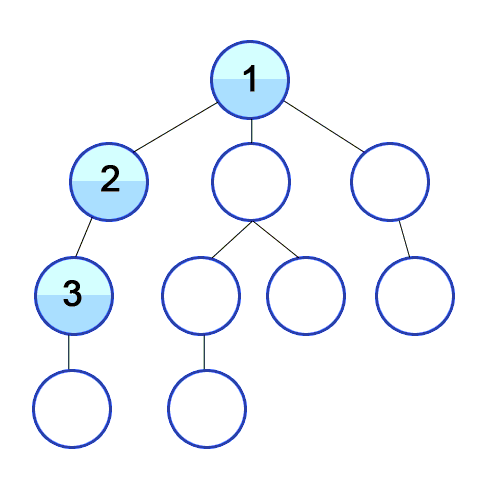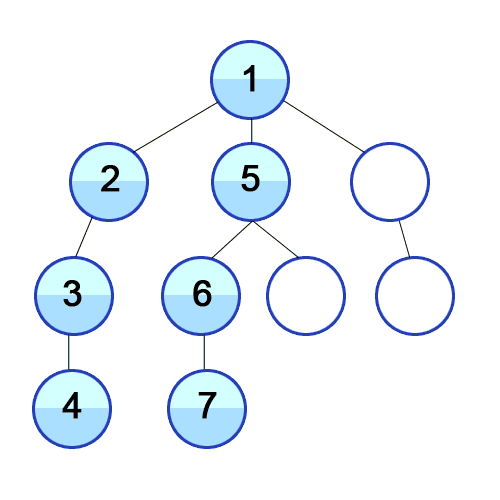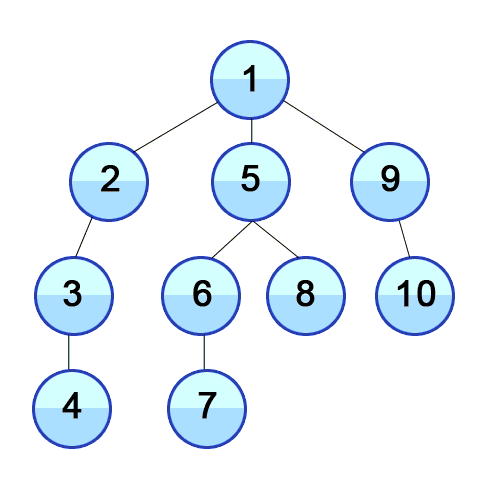
Breadth-first search traverses the nodes in each layer of the tree before traversing to the next layer.

animation showing 8 nodes being explored via breadth-first search

Breadth-first search is generally implemented using a queue:

void breadthFirstSearch(Node head) {
  Deque<Node> nodeQueue = new ArrayDeque<>();
  nodeQueue.add(head);

  while(!nodeQueue.isEmpty()){
    Node node = nodeQueue.remove();

    // Do something with the current node.
    System.out.println(node.value);

    // Add each child to the queue.
    for(Node child : node.children) {
      nodeQueue.add(child);
    }
  }
}

Solving Tree Problems

Tree problems come in many shapes and sizes, but you can approach them with a few techniques.

  1. First, think about what kind of tree you’re working with. Is it a binary tree, or can each node have more than two children? Is it a binary search tree, or can the content of the nodes appear in any order?
  2. Next, talk through your different options for traversing the tree. Does depth-first search make sense, or do you need breadth-first search? What are the pros and cons? What tradeoffs are you making?
  3. What action do you need to take for each node? Are you searching for a particular value, or are you building up a path of nodes? If you’re using recursion, what’s your base case?

Remember that interviews are meant to be conversations, so try to talk through what you’re thinking. Even naming various techniques, like mentioning that you’re thinking about depth-first search vs breadth-first search, can score you bonus points!

Learn More

Practice Problems

Traversal Practice Problems

Previous:
Linked Lists
Next:
Graphs

Comments

Happy Coding is a community of folks just like you learning about coding.
Do you have a comment or question? Post it here!

Comments are powered by the Happy Coding forum. This page has a corresponding forum post, and replies to that post show up as comments here. Click the button above to go to the forum to post a comment!